Scalar and vector quantities

Scientists often make measurements. The physical quantities they measure fall into two categories: scalars and vectors. Scalar and vector quantities are treated differently in calculations.

Scalar quantities

A physical quantity is something that can be measured. Scalar quantities only have a magnitude or size.

Examples of scalar quantities

Some examples of scalar quantities include:

• temperature – eg 10 degrees Celsius (°C)
• mass – eg 5 kilograms (kg)
• energy – eg 2,000 joules (J)
• distance – eg 19 metres (m)
• speed – eg 8 metres per second (m/s)
• density – eg 1,500 kilograms per metre cubed (kg/m³)

Calculations involving scalar quantities

Adding scalars

The sum of scalar quantities can be found by adding their values together.

Example

Calculate the total mass of a 75 kg climber carrying a 15 kg backpack.

75 kg + 15 kg = 90 kg

Subtracting scalars

Scalar quantities can be subtracted by subtracting one value from another.

Example

A room is heated from 12°C to 21°C using a heater. Calculate the increase in temperature.

21°C – 12°C = 9°C

Vector quantities

Vector quantities have both magnitude and an associated direction. This makes them different from scalar quantities, which just have magnitude.

Examples of vector quantities

Some examples of vector quantities include:

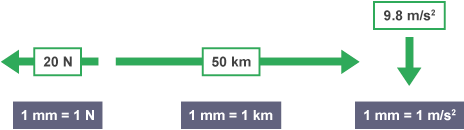
• force – eg 20 newtons (N) to the left
• weight – eg 600 newtons (N) downwards
• displacement – eg 50 kilometres (km) east
• velocity – eg 11 metres per second (m/s) upwards
• acceleration – eg 9.8 metres per second squared (m/s²) downwards
• momentum – eg 250 kilogram metres per second (kg m/s) south west

The direction of a vector can be given in a written description, or drawn as an arrow. The length of an arrow represents the magnitude of the quantity. If one arrow is twice as long as another, it represents a force which has twice the magnitude.

The diagrams show three examples of vectors, drawn to different scales.

Motion

The movement of objects can be described using motion graphs and numerical values. These are both used to help in the design of faster and more efficient vehicles.

Motion in a straight line

Distance is how far an object moves. It does not include an associated direction, so distance is a scalar quantity.

Speed is the rate of change of distance – it is the distance travelled per unit of time. Like distance, speed also does not have an associated direction, so it is a scalar quantity.

Typical speeds

When people walk, run, or travel in a car their speed will change. They may speed up, slow down or pause for traffic.

Some typical values for speed in metres per second (m/s) include:

Method of travel	Typical speed (m/s)
Walking	1.5
Running	3
Cycling	6
Car	13-30
Train	50
Aeroplane	250

It is not only moving objects that have varying speed. The speed of the wind and the speed of sound also vary. A typical value for the speed of sound in air is about 330 m/s. A light breeze moves at perhaps 3 m/s, but a gale would be more than 20 m/s.

Calculations involving space, distance and time

The speed of an object can be calculated using the equation:

(average)speed=distance travelled/time taken

v=x/t

The distance travelled by an object moving at constant speed can be calculated using the equation:

distance travelled = average speed × time taken

x=vt

This is when:

• distance travelled (x) is measured in metres (m)
• speed (v) is measured in metres per second (m/s)
• time taken (t) is measured in seconds (s)

Distance-time graphs

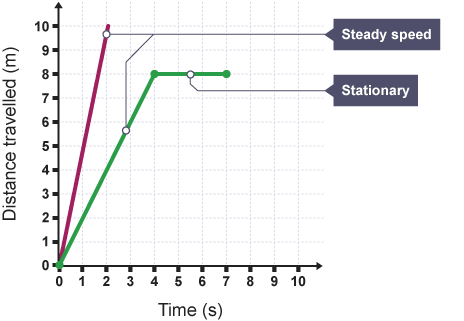
For a moving object, the distance travelled can be represented by a distance-time graph.

A horizontal line on a distance-time graph shows that the object is stationary (not moving), while a sloping line on a distance-time graph shows that the object is moving.

The speed of an object can be calculated from the gradient of a distance-time graph.

The greater the gradient (and the steeper the line) the faster the object is moving.

Acceleration

Acceleration is the rate of change of velocity. It is the amount that velocity changes per unit time.

If an object accelerates from an initial velocity (u) up to a final velocity (v) then the average acceleration of an object can be calculated using the equation:

acceleration = change in velocity/time taken

α = (v − u/)t

This is when:

• acceleration (α) is measured in metres per second squared (m/s²)
• change in velocity (v – u) is measured in metres per second (m/s)
• time taken (t) is measured in seconds (s)

If an object is slowing down, it is decelerating (and its acceleration has a negative value).